Circle packing in an isosceles right triangle
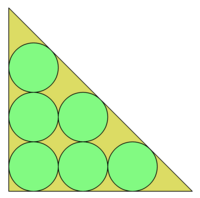
Alright kiddo, imagine you have a right triangle that has two sides that are the same length, and one side that's longer. This is called an isosceles right triangle, because the two smaller sides are equal and one of the angles is a right angle (like a corner of a square).
Now let's talk about circles! You know what a circle looks like, right? It's a round shape that's sort of like a tire or donut. Well, if you were to try and fit as many circles as you could inside that isosceles right triangle without letting any of them overlap or go outside the triangle, that's called "circle packing".
Circle packing is like a puzzle, and it's kind of like playing Tetris with circles instead of blocks. You have to figure out the best way to fit them all together so that there are no gaps or overlaps.
But there's a catch! The circles can't just be any size - they all have to be the same size. That makes it much harder to fit them all in there.
Circle packing in an isosceles right triangle is actually a really interesting mathematical problem, and it's fun to see how many circles you can fit in there and how they all fit together. So it's like a big puzzle that's also a math problem!
Now let's talk about circles! You know what a circle looks like, right? It's a round shape that's sort of like a tire or donut. Well, if you were to try and fit as many circles as you could inside that isosceles right triangle without letting any of them overlap or go outside the triangle, that's called "circle packing".
Circle packing is like a puzzle, and it's kind of like playing Tetris with circles instead of blocks. You have to figure out the best way to fit them all together so that there are no gaps or overlaps.
But there's a catch! The circles can't just be any size - they all have to be the same size. That makes it much harder to fit them all in there.
Circle packing in an isosceles right triangle is actually a really interesting mathematical problem, and it's fun to see how many circles you can fit in there and how they all fit together. So it's like a big puzzle that's also a math problem!
