Close-packing of equal spheres

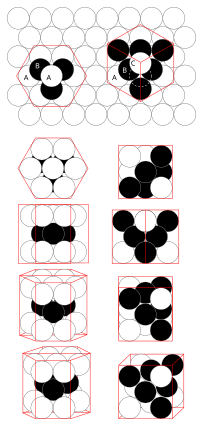
Imagine you have a bunch of toy balls that are all exactly the same size. These balls can only touch each other at their surfaces, and they can't overlap or go through each other. How could you arrange them so that you fit the most balls in a small space?

One way is to start by placing one ball in the center of a square or hexagon. Then, you can add more balls around it in layers, like building a pyramid or a tower. Each layer has a pattern that repeats across the whole layer, and that pattern is rotated slightly from the pattern of the layer below it. This way, each ball touches exactly six other balls (in the case of a hexagonal pattern) or four other balls (in the case of a square pattern).

This pattern of arranging balls is called "close-packing of equal spheres." Scientists call it a "densest packing" because it puts the most balls in the smallest possible space. Mathematicians have proven that the close-packing of spheres in three dimensions is the most efficient way to fill space with identical spheres.

This idea of close-packing is actually very important in chemistry and materials science, because atoms and molecules can also be thought of as tiny spheres that interact with each other in similar ways. Understanding how close-packing works can help scientists make new materials with the properties they need.