Confocal conic sections

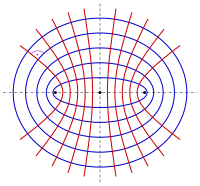
Imagine you're standing in a room with a flashlight. You shine the flashlight around the room and it creates a big circle on the wall. When you move the flashlight closer to the wall, the circle gets smaller. Confocal conic sections work kind of like that flashlight.

Confocal conic sections are a group of shapes that are created by slicing a cone at different angles. A cone is like an ice cream cone – it starts out wide on one end and gets narrower on the other end. When you slice a cone, you can create different shapes depending on the angle of the cut.

Now, imagine that you have two cones that are stacked on top of each other, with the smaller tip of one cone touching the larger end of the other cone. These two cones are said to be "confocal" because they share the same focus point – the point where a beam of light would converge if you shone it through both cones.

When you slice through these two confocal cones at certain angles, you create different shapes called conic sections. These shapes include circles, ellipses, parabolas, and hyperbolas.

For example, if you slice through the cones at a perpendicular angle, you'll create a circle. But if you slice through them at a slight angle, you might create an ellipse – a shape that's like a stretched-out circle. If you slice through them at a steeper angle, you might create a parabola – a shape that's kind of like a smiley face. And if you slice through them at an even steeper angle, you might create a hyperbola – a shape that looks like two mirrored arcs that never quite meet.

So, in summary, confocal conic sections are different shapes that you can create by slicing through two stacked cones at different angles. These shapes include circles, ellipses, parabolas, and hyperbolas.