Dendroid (topology)
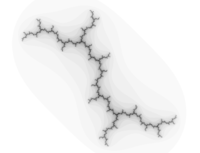
Imagine you have a bunch of sticks that you want to connect to make a big structure. You start by connecting two sticks with a joint, and then you connect more sticks to those two, making branches. Each time you make a branch, you can add more sticks to that branch, and keep going until you have a big tree-like structure made up of lots and lots of smaller sticks.
This is what a dendroid is - a big, branching structure made up of smaller branches. In mathematics, a dendroid is a type of topological space that has this tree-like structure. It's like a network of connections, where each connection is a branch that keeps branching out into smaller and smaller connections.
The idea of dendroids is important in topology because they help us understand the ways that shapes and spaces can be connected. By studying the properties of dendroids, mathematicians can learn more about the structure of different types of spaces and how they behave under different conditions.
This is what a dendroid is - a big, branching structure made up of smaller branches. In mathematics, a dendroid is a type of topological space that has this tree-like structure. It's like a network of connections, where each connection is a branch that keeps branching out into smaller and smaller connections.
The idea of dendroids is important in topology because they help us understand the ways that shapes and spaces can be connected. By studying the properties of dendroids, mathematicians can learn more about the structure of different types of spaces and how they behave under different conditions.
