Finite-dimensional vector space

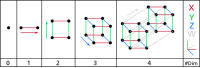
Okay, so you know how you play with blocks or toy cars and you can move them around in different directions? And you can also make them bigger or smaller by adding or removing more pieces?

Well, imagine that instead of blocks, we have things called vectors, which are like arrows. And instead of moving them around or making them bigger or smaller, we can do some math operations with them, like adding or subtracting, and multiplying by numbers.

A finite-dimensional vector space is like a big collection of these vectors that we can do these math operations with. But the important thing is that we can only use a certain number of arrows (or vectors), and we can't add more as we please. It's like playing with a set of blocks with a limited number of pieces.

So, in summary, a finite-dimensional vector space is a collection of arrows (or vectors) that we can play with by doing some math operations with them, but we can only use a certain number of arrows, and we can't add more as we please.