Folded cube graph

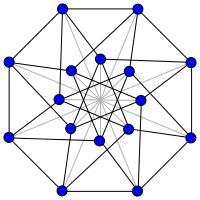
Imagine you have a cube, which is like a box with six sides. Now, imagine folding up that cube in different ways so that some of the sides are touching or overlapping. This creates a folded cube, which is a cube that has been bent and twisted into a new shape.

A folded cube graph is a way to represent this shape on a piece of paper. Instead of drawing a picture of the folded cube, we use lines and dots to show how the different parts of the cube are connected. The dots represent the vertices, or corners, of the cube, and the lines represent the edges, or sides, of the cube.

The folded cube graph can be useful for understanding how the different parts of the cube fit together, and for studying different types of folding patterns or symmetries. By looking at the graph, we can see which vertices and edges are connected, and how they are connected, even if we can't see the actual cube itself.

It's like drawing a map of a place you've never been to before. The map shows you the different streets and buildings, and how they are connected, so that even if you've never been there before, you can still understand how everything fits together. The folded cube graph does the same thing, by giving us a visual representation of a complex 3D shape that we can easily understand and study.