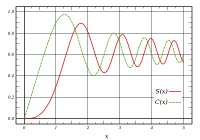
Fresnel integral

So, imagine you're playing with a ball outside and it starts raining. You still want to play with the ball but you can't see it clearly because the rain is making everything look blurry. That's kind of like what a fresnel integral does.

A fresnel integral is a way of calculating how light waves change when they pass through a curved surface or edge. It helps us understand how things like lenses and mirrors affect the way we see things.

To understand it better, let's think about a wave of light traveling through the air. When it hits the edge of a surface, like a lens or a mirror, some of the light is reflected and some of it is refracted (which means it bends).

The fresnel integral helps us calculate exactly how much of the light wave is reflected and how much is refracted, depending on the angle of the wave and the angle of the edge it hits.

Basically, it's like a math formula that helps us predict how light will behave when it hits a curved surface. And that's important because it helps us design things like lenses and mirrors for cameras, telescopes, and other optical devices that help us see things better.

So now, the next time you're playing with a ball outside, you can remember how a fresnel integral helps us see things better through lenses and mirrors!