Gauss circle problem

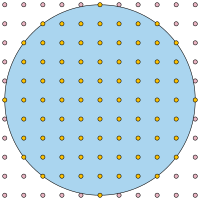
The Gauss Circle Problem is a math puzzle where we count the number of points that are inside a circle if all the points have whole number coordinates. Imagine drawing a big circle on a piece of paper and putting a dot in the center. If we draw lines that are one unit apart from each other and create a grid of squares, we'll notice that some of these squares are completely inside the circle, some are outside the circle, and some squares are partially inside the circle.

Now, if we wanted to find out how many points with whole number coordinates are inside the circle, that's where it gets tricky. It's not easy to simply count all those dots, but we can use a mathematical formula developed by Carl Friedrich Gauss (hence the name "Gauss Circle Problem") to estimate it.

In simple terms, Gauss figured out a way to use pi (3.14159...) and other mathematical concepts to come up with a really close estimate of how many dots are inside the circle. But because the circle is so big, and there are so many dots to count, it's still a pretty challenging problem that mathematicians are still working on today.