Hilbert transform in the complex plane
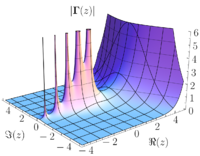
The Hilbert Transform is a fancy way of talking about some math that helps us to analyze signals like sounds or vibrations. Imagine you have a toy xylophone in front of you and you hit it with a mallet. The sound that comes out can be broken down into different parts called frequencies. Each frequency is like a little wave and all of them added together make the sound you hear.
The Hilbert Transform is a way of taking that sound and separating out each of those little waves so we can look at them more closely. We do this by drawing a line on a special graph called the complex plane. The complex plane is like a big sheet of paper with two lines, one going left and right and one going up and down. We use this graph to represent complex numbers, or numbers that have two parts: a real part and an imaginary part.
When we apply the Hilbert Transform to our sound, we take the real part of the waves and plot them on one line of the complex plane, and the imaginary part on another line. Then we connect each point on the graph with a straight line to its "mirror image" across the imaginary axis. This creates a special shape called an analytic signal. This signal is useful because it tells us the frequency and phase of the original sound.
So, in simpler terms, the Hilbert Transform is like taking a toy xylophone, breaking down the sound it makes into different little waves, and drawing those waves on a very special piece of paper. Once we do this, we can learn more about the sound and how it's made up.
The Hilbert Transform is a way of taking that sound and separating out each of those little waves so we can look at them more closely. We do this by drawing a line on a special graph called the complex plane. The complex plane is like a big sheet of paper with two lines, one going left and right and one going up and down. We use this graph to represent complex numbers, or numbers that have two parts: a real part and an imaginary part.
When we apply the Hilbert Transform to our sound, we take the real part of the waves and plot them on one line of the complex plane, and the imaginary part on another line. Then we connect each point on the graph with a straight line to its "mirror image" across the imaginary axis. This creates a special shape called an analytic signal. This signal is useful because it tells us the frequency and phase of the original sound.
So, in simpler terms, the Hilbert Transform is like taking a toy xylophone, breaking down the sound it makes into different little waves, and drawing those waves on a very special piece of paper. Once we do this, we can learn more about the sound and how it's made up.
