Homotopy cofiber

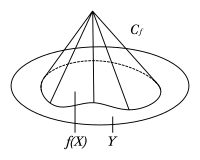
Imagine you have two pictures. Let's call the first picture A and the second picture B. They are kind of similar, but not exactly the same.

Now, let's say you want to make a new picture that is a sort of combination of A and B. But instead of just mashing them together, you want to make it look like A slowly transforms into B.

That's what we call a "homotopy." It's like a fancy way of saying we're going to make a smooth transition from one picture to the other.

The "cofiber" part is a little trickier. But basically, imagine we have a bunch of strings tied together. We could say that they are all "connected" in some way.

Now, imagine we cut one of the strings. The other strings are still connected to each other, but they are not connected to the string we cut anymore. That "disconnected" string is kinda like the cofiber.

So when people talk about a "homotopy cofiber," what they mean is that they're using a fancy math trick to make a smooth transition between two pictures, and then looking at what happens when you "cut" the picture in a certain way.

It's a concept that is important in certain branches of math and science, but for now, just remember that a homotopy cofiber is like a smooth transition between two things, with an interesting "cutting" property.