Inequality of arithmetic and geometric means

Okay kiddo, Arithmetic mean is like collecting strawberries from a farm, you pick different sizes of strawberries, and then you calculate the average size of all the strawberries you picked. That's arithmetic mean!

Now coming to Geometric mean, imagine you are planting strawberry seeds in your garden. Some seeds will grow big, and some will grow small. Geometric mean helps you determine the average size of strawberries that are harvested from each seed.

So what's the inequality of arithmetic and geometric means? Well, sometimes when you compare the arithmetic mean and geometric mean, the geometric mean will always be smaller than the arithmetic mean. Isn't that strange? Here's why:

When you add a group of numbers and divide by the number of items (arithmetic mean), the result will be bigger than when you multiply those same numbers and take the nth root (geometric mean).

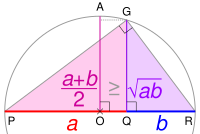
So the inequality of arithmetic and geometric means states that the arithmetic mean is always greater than or equal to the geometric mean of a set of positive numbers.

But why does this happen? Think of it like this; when you add numbers, the sum gets bigger and bigger, but when you multiply numbers, the product gets smaller and smaller. And since the product is smaller, taking the nth root will also be smaller than the arithmetic mean.

So remember, arithmetic mean is bigger than geometric mean, so if you want to know the average size for a group of numbers, use arithmetic mean, and if you want to know the average effect for a group of numbers, use geometric mean!