Kosnita theorem
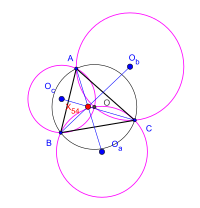
The kosnita theorem is a fancy math idea that helps us understand certain kinds of triangles. A triangle is a shape with three sides and three corners. Now, in some triangles, we can draw a special line from each corner to the opposite side, and where these lines all meet is a point in the middle of the triangle. This point is called the "circumcenter".
The kosnita theorem says that if we draw some more lines in the triangle, in a special way, they will all meet at a different point. This new point is called the "kosnita point".
To understand this better, imagine you are drawing a triangle on a piece of paper. First, draw the three sides of the triangle. Then, for each corner of the triangle, draw a line that goes straight across to the opposite side of the triangle. These are called the "altitudes" of the triangle.
Now, we can draw some more lines. Start at any corner of the triangle and draw a line that goes through the midpoint of the opposite side. The midpoint is the exact middle of the side, so this line is cutting the side exactly in half. Then, draw another line that goes from the same corner of the triangle, through the opposite corner, and meets the first line we just drew.
If we do this for all three corners of the triangle, we will end up with three lines that all meet at a point. This point is the kosnita point.
Now, you might be wondering what's the point of all this? Well, it turns out that the kosnita point and the circumcenter are related in a really cool way. If we draw a line that goes through both of these points, it will cut the triangle in half! This means that the two sides of the triangle on either side of the line will be exactly equal in length.
So, the kosnita theorem is all about special lines we can draw in a triangle that help us understand its geometry better.
The kosnita theorem says that if we draw some more lines in the triangle, in a special way, they will all meet at a different point. This new point is called the "kosnita point".
To understand this better, imagine you are drawing a triangle on a piece of paper. First, draw the three sides of the triangle. Then, for each corner of the triangle, draw a line that goes straight across to the opposite side of the triangle. These are called the "altitudes" of the triangle.
Now, we can draw some more lines. Start at any corner of the triangle and draw a line that goes through the midpoint of the opposite side. The midpoint is the exact middle of the side, so this line is cutting the side exactly in half. Then, draw another line that goes from the same corner of the triangle, through the opposite corner, and meets the first line we just drew.
If we do this for all three corners of the triangle, we will end up with three lines that all meet at a point. This point is the kosnita point.
Now, you might be wondering what's the point of all this? Well, it turns out that the kosnita point and the circumcenter are related in a really cool way. If we draw a line that goes through both of these points, it will cut the triangle in half! This means that the two sides of the triangle on either side of the line will be exactly equal in length.
So, the kosnita theorem is all about special lines we can draw in a triangle that help us understand its geometry better.
