Linear dependence

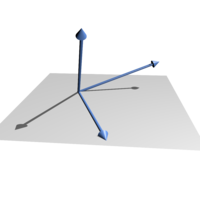
Linear dependence happens when some things are connected to each other in a way that if you change one thing, it changes the others too.

For example, imagine you have some toy cars: a red one, a blue one, and a green one. Let's say you want to make a car parade, but you only want to use two cars. Can you pick any two cars and still have a parade?

If you pick the red car and the blue car, you can have a parade. But if you pick the red car and the green car, you can't really have a parade because the cars don't match. That's because the red and blue cars are "dependent" on each other - they work together to make a parade. But the red and green cars are "independent" of each other - they don't work together to make a parade.

In math, we use vectors (which are just fancy arrows) to understand linear dependence. If you have two vectors, they are linearly dependent if one of them can be made by multiplying the other by a number and adding or subtracting them. So just like the red and blue cars work together to make a parade, two vectors can work together to make other vectors. And if they can't work together in this way, then they are linearly independent.