Mittag-Leffler function

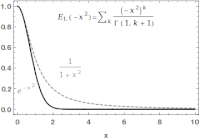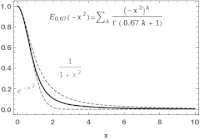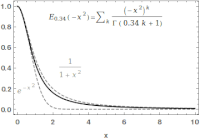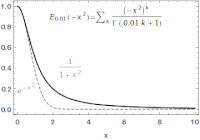
Imagine you have a bunch of colorful blocks, and you want to stack them up in a tower. But instead of just stacking them in a neat, straight line, you want to be more creative with how you arrange them. You might have some blocks sticking out at angles, or some blocks stacked higher than others.

Now, let's say you want to figure out how tall your tower is at any given point. This is where the Mittag-Leffler function comes in. It's a mathematical function that helps you determine the height of your tower at specific points.

But instead of just dealing with colorful blocks, the Mittag-Leffler function works with complex numbers. These are numbers that have both a real component (like 3 or -5) and an imaginary component (like i, which stands for the square root of -1).

The Mittag-Leffler function works by taking a complex number and plugging it into an equation that involves other complex numbers called poles. These poles are kind of like the "peak" points in your tower of blocks. They're the spots where the tower has the highest blocks, or where blocks might stick out at odd angles.

By plugging your complex number into the equation involving these poles, the Mittag-Leffler function can tell you how tall your "tower" is at that point. It's a useful tool in complex analysis, which is all about studying complex functions (like the Mittag-Leffler function) and how they behave.

So, in summary: imagine you have a tower of colorful blocks that's arranged in a creative, non-linear way. The Mittag-Leffler function is like a tool that helps you figure out how tall your tower is at specific points by plugging a complex number into an equation involving other complex numbers called poles.