Ramanujan's master theorem
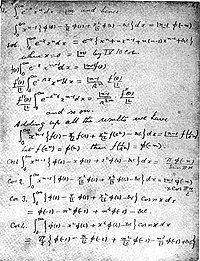
Ramanujan's master theorem is a really cool math thing that helps us find out how many ways we can divide up something called a partition.
Do you know what a partition is? It's when you take a big number and break it up into smaller numbers. For example, if you have the number 4, you can partition it into 1+1+1+1 or 2+2 or 1+1+2 or 1+3 or 4.
Now, sometimes we want to know how many ways we can partition a certain number. This is where Ramanujan's master theorem comes in.
Picture a circle with a bunch of numbers around the edge, like a clock. You can pick any number on the circle and start counting clockwise. Let's say you pick the number 12. Then you start counting: 12, 10, 7, 3, 12. You can keep doing this until you hit the number 12 again.
Now, let's say you keep doing this for every number on the circle. You'll get a bunch of different counts, right? Ramanujan's master theorem says that if you add up all those counts and divide by the number of numbers on the circle, you'll get the answer to how many ways you can partition the number you started with.
It might sound a little confusing, but basically Ramanujan's master theorem helps us figure out how many ways we can break a number up into smaller numbers. Pretty cool, huh?
Do you know what a partition is? It's when you take a big number and break it up into smaller numbers. For example, if you have the number 4, you can partition it into 1+1+1+1 or 2+2 or 1+1+2 or 1+3 or 4.
Now, sometimes we want to know how many ways we can partition a certain number. This is where Ramanujan's master theorem comes in.
Picture a circle with a bunch of numbers around the edge, like a clock. You can pick any number on the circle and start counting clockwise. Let's say you pick the number 12. Then you start counting: 12, 10, 7, 3, 12. You can keep doing this until you hit the number 12 again.
Now, let's say you keep doing this for every number on the circle. You'll get a bunch of different counts, right? Ramanujan's master theorem says that if you add up all those counts and divide by the number of numbers on the circle, you'll get the answer to how many ways you can partition the number you started with.
It might sound a little confusing, but basically Ramanujan's master theorem helps us figure out how many ways we can break a number up into smaller numbers. Pretty cool, huh?
