Residue theorem

Imagine you have a big playground and you want to count all the kids playing there. One way to do this is to count them one by one, which could take a long time. Another way is to create groups of kids and count the number of groups instead of each kid. This makes counting easier and faster.

Similarly, the residue theorem is a way to make counting the zeros or poles of a complex function easier by grouping them together. In complex analysis, complex functions have complex zeros and poles which can be difficult to evaluate individually. The residue theorem provides a shortcut to calculate the sum of some or all of those zeros or poles.

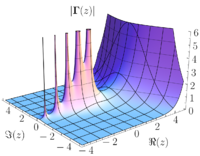
Here's how the residue theorem works: Imagine you have a complicated function represented by a graphic circle. Within the circle there may be points where the function is undefined, or there might be values of x that would make the function go crazy if you plug them in. These are called singularities, and they can either be zeros or poles.

Now, if we draw a small circle around each singularity (a circle is a way to measure distance from a point), we can measure the 'group' of all values that are in the circle together. We say that the sum of all of these values is 2πi multiplied by the residue of the point.

So instead of adding up all the singularities one by one, we can just add the residue of the points that we manage to group together. This makes finding the sum of the zeros and poles of the complex function much easier, and that's the residue theorem in action!

In summary, just as grouping kids together helps count them more efficiently, grouping singularities together around a circle helps count them more easily by using the residue theorem.