Sleeping Beauty problem

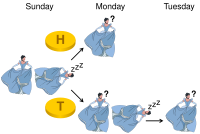
The Sleeping Beauty Problem is a question that tries to figure out how much we should trust the uncertainty of probability. It goes like this: Sleeping Beauty is put to sleep on Sunday night. When she wakes up, she is asked whether a coin has been flipped while she was asleep. If the coin is heads, she is asked on Monday. If the coin is tails, she is asked on both Monday and Tuesday. Suppose the coin is flipped while Sleeping Beauty is asleep and it comes up tails. What is the probability that it is Monday?

The answer to this question can be confusing! There are two views of this situation. The first view says that there is a 1 in 2 chance that it's Monday. The second view says that there is a 2 in 3 chance that it's Monday.

Most people believe the first view, that it is a 1 in 2 chance that it is Monday. This is because Sleeping Beauty knows nothing about the coin flip and so there is still the same chance when she wakes up that it is either Monday or Tuesday, the same as before she went to sleep.

The second view is a bit more complicated. It says that since Sleeping Beauty will only be asked the question if the coin lands on tails, that means that the chance that it's Monday is higher. This is because two out of the three possible outcomes (head and two tails) mean that it is Monday, whereas only one out of the three outcomes (head) means that it is Tuesday. So there is actually a 2 in 3 chance that it is Monday.