Stirling's approximation
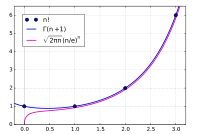
Hey there kiddo! Have you ever heard of a man called James Stirling? He was a smart guy who figured out a cool trick that helps us estimate big numbers without doing a ton of math. This trick is called Stirling's Approximation.
Now, imagine you have a really big number like 100! (that's 100 times 99 times 98 times 97... and so on, all the way down to 1). If we wanted to figure out the exact value of this number, we would have to do A LOT of multiplication, which could take us forever. But Stirling's Approximation says we can get a pretty good estimate of 100! by using a simple formula:
100! ≈ (√(2π)*10100)*(n/e)^100
Wow, that looks like a lot of math, but let's break it down. The tiny number 'e' is a special number that pops up a lot in math. It is equal to about 2.71828, but we won't worry too much about that for now.
The formula is telling us to take the value of 'n' (which is our big number like 100 in this case), divide it by 'e', and then raise that result to the power of 'n'. Then, we multiply that answer by (√(2π)*10100), which is just a fancy number that helps make our estimate more accurate.
When we plug in 100 for 'n', we get:
100! ≈ (√(2π)*10^100)*(100/e)^100
This may still look like a lot of numbers, but we can use Stirling's Approximation to estimate this number without doing all the multiplication.
So kiddo, you see how Stirling's Approximation helps us make good guesses for big numbers like 100!? We can use this trick to estimate all sorts of complicated calculations with ease. Pretty cool, huh?
Now, imagine you have a really big number like 100! (that's 100 times 99 times 98 times 97... and so on, all the way down to 1). If we wanted to figure out the exact value of this number, we would have to do A LOT of multiplication, which could take us forever. But Stirling's Approximation says we can get a pretty good estimate of 100! by using a simple formula:
100! ≈ (√(2π)*10100)*(n/e)^100
Wow, that looks like a lot of math, but let's break it down. The tiny number 'e' is a special number that pops up a lot in math. It is equal to about 2.71828, but we won't worry too much about that for now.
The formula is telling us to take the value of 'n' (which is our big number like 100 in this case), divide it by 'e', and then raise that result to the power of 'n'. Then, we multiply that answer by (√(2π)*10100), which is just a fancy number that helps make our estimate more accurate.
When we plug in 100 for 'n', we get:
100! ≈ (√(2π)*10^100)*(100/e)^100
This may still look like a lot of numbers, but we can use Stirling's Approximation to estimate this number without doing all the multiplication.
So kiddo, you see how Stirling's Approximation helps us make good guesses for big numbers like 100!? We can use this trick to estimate all sorts of complicated calculations with ease. Pretty cool, huh?
Related topics others have asked about:
