Barycentric subdivision
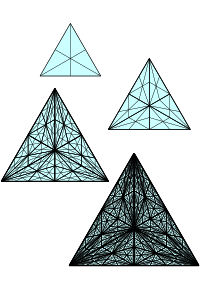
Barycentric subdivision is like cutting a shape into smaller and smaller pieces by drawing lines from the corners to the middle.
Imagine you have a triangle. To barycentrically subdivide it, you draw lines from each corner to the middle of the opposite side. You end up with 3 new smaller triangles inside the big triangle.
Then, for each of those new triangles, you repeat the process by drawing lines from each corner to the middle of the opposite side. So now you have 9 even smaller triangles inside the big triangle.
You keep doing this over and over until the pieces are small enough as you want them.
Barycentric subdivision is important in lots of areas of math, like geometry and topology because it helps break down shapes into smaller and more manageable pieces, which makes them easier to study and understand. It's like taking a big problem and breaking it down into smaller, easier-to-solve problems.
Imagine you have a triangle. To barycentrically subdivide it, you draw lines from each corner to the middle of the opposite side. You end up with 3 new smaller triangles inside the big triangle.
Then, for each of those new triangles, you repeat the process by drawing lines from each corner to the middle of the opposite side. So now you have 9 even smaller triangles inside the big triangle.
You keep doing this over and over until the pieces are small enough as you want them.
Barycentric subdivision is important in lots of areas of math, like geometry and topology because it helps break down shapes into smaller and more manageable pieces, which makes them easier to study and understand. It's like taking a big problem and breaking it down into smaller, easier-to-solve problems.
