Chebyshev nodes
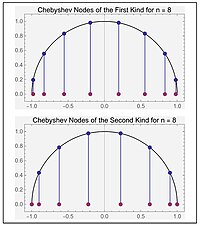
Chebyshev nodes are points on a line or curve that are arranged in a very special way. Instead of having points that are evenly spaced apart, like tic-tac-toe marks on a piece of paper, these points are much smarter! They are positioned in a way that makes them very useful for doing certain math problems, especially when it comes to things like approximating functions, which means finding a good guess for what a curve or line might look like.
Now, imagine if you were to draw a line on a piece of paper and you wanted to put 5 points on it, but you wanted to do it in a way that’s really smart. What would you do? Well, first you would want to make sure that the points were as spread out as possible, so they weren’t too close together. You would also want to make sure that you put the points where they could tell you the most about the shape of the line.
That's where Chebyshev nodes come in! They are really good at helping us find those special points. They are arranged on the line in such a way that any two of them are as far apart as possible. So, if you took the first and last point and stretched a rubberband between them, you would find that it’s as tight as can be. This is called being ‘maximally separated’.
The reason we care about this special type of point is because if you use them to approximate a function, like a curve or line, you can be sure that your guess will be really good, and not just an estimate. So, if you’re building something, like a bridge, and you need to know the exact shape of a certain curve, you can use these points to figure out what it is.
Overall, Chebyshev nodes are really handy when you want to figure out what a curve or line looks like. They’re like a secret code that helps you unlock the shape of a function with less work than other methods!
Now, imagine if you were to draw a line on a piece of paper and you wanted to put 5 points on it, but you wanted to do it in a way that’s really smart. What would you do? Well, first you would want to make sure that the points were as spread out as possible, so they weren’t too close together. You would also want to make sure that you put the points where they could tell you the most about the shape of the line.
That's where Chebyshev nodes come in! They are really good at helping us find those special points. They are arranged on the line in such a way that any two of them are as far apart as possible. So, if you took the first and last point and stretched a rubberband between them, you would find that it’s as tight as can be. This is called being ‘maximally separated’.
The reason we care about this special type of point is because if you use them to approximate a function, like a curve or line, you can be sure that your guess will be really good, and not just an estimate. So, if you’re building something, like a bridge, and you need to know the exact shape of a certain curve, you can use these points to figure out what it is.
Overall, Chebyshev nodes are really handy when you want to figure out what a curve or line looks like. They’re like a secret code that helps you unlock the shape of a function with less work than other methods!
