Codomain

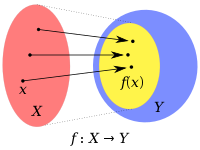
Have you ever played a game where you have to match shapes or colors? Let's say you have a set of circles and squares, and you need to match them with the right color. Your job is to put all the circles with blue dots and all the squares with red dots. That's like a big rule you need to follow.

Now imagine you have another set of circles and squares. These are just shapes, they don't have any dots or colors. But you still need to match them in some way. This time, you're told to put all the circles in one box and all the squares in another box. That's another rule you need to follow.

The first set of rules is called a "function," and the second set is called a "codomain." The codomain is like a box where you put all the shapes that don't have a special color or dot on them. It's the set of all possible outputs that the function can produce, even if they don't match any of the specific rules you've been given.

So, when we talk about a codomain in math, we're talking about all the possible outputs of a function, even if they don't have a specific "matching rule" that we've been given. It's like a big box where we put all the shapes that don't fit into the colored-dot box.