Conformally flat manifold

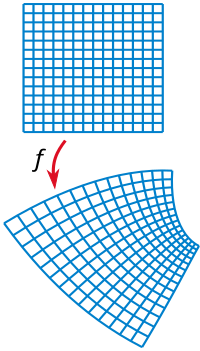
Imagine you are playing with Play-Doh and roll it out to create a flat surface. Now imagine you lift up the edges of the Play-Doh so that it becomes curved or bent in some places. This is like a manifold, which is a special type of mathematical object that represents a space that can be curved or bent in certain ways.

Now, let's add another rule: we have to be able to use a special tool to flatten the bent parts of the Play-Doh without making any cuts or tears. This is called a conformal transformation, and it means that we are allowed to stretch or shrink the Play-Doh in different directions, but we cannot actually change the shape of the surface.

A manifold that can be transformed into a flat surface using only conformal transformations is called a conformally flat manifold. Just like with the Play-Doh, we can think of this as a space that can be bent or curved, but can still be considered "flat" in some special sense. This can be useful in certain areas of physics and geometry, where we want to study spaces that are curved in certain ways while still maintaining certain important properties.