Conjugate gradient method

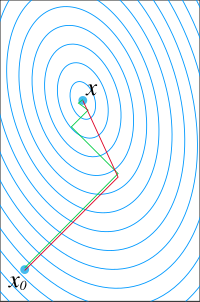
Imagine you have a big math problem you need to solve, but it's too complicated to solve all at once. It's like a giant puzzle, and you need to break it down into smaller pieces so that you can solve each part one by one. This is where the conjugate gradient method comes in handy.

The conjugate gradient method is a way of solving big math problems by breaking them down into smaller pieces and solving each part step by step. To start, you need to have an initial guess for the solution. This is like having a starting point for your puzzle. You start with a guess at what the answer might be.

Then, you take a step towards the correct answer by finding a search direction. This is like looking at the puzzle and figuring out which piece to work on next. You choose a direction that will bring you closer to the answer, and you take a small step in that direction.

Next, you need to figure out how far to move in that direction. You do this by finding the minimum point in that direction, which is like finding the edge of a puzzle piece that fits perfectly with the piece you're working on. You move in that direction until you find the minimum point.

Then, you update your guess for the solution based on the minimum value you found. This is like putting the piece in place and seeing how it fits with the other pieces. You go back to your initial guess and make it more accurate based on the information you just found.

You repeat this process, moving in different directions each time, until you get closer and closer to the correct answer. It's like working on different parts of the puzzle until you eventually solve the whole thing.

Overall, the conjugate gradient method is a way of breaking down big math problems into smaller, more manageable parts and solving each part step by step. Just like how you would solve a puzzle piece by piece until you complete the whole thing.