Consistent estimator

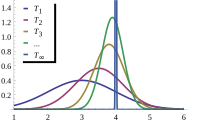
A consistent estimator is like a guessing game. Imagine you have a jar filled with different candies, and you want to know how many candies are inside the jar. You might take a few guesses, but you know you need to make your guesses better to get closer to the real number of candies.

Similarly, in statistics, we use sampling to estimate something about a population. For example, let's say we want to estimate the average weight of all cats in a city. We could collect data by weighing a few cats, but we know that our estimate might not be exactly right. So, we take more samples, and we keep improving our estimate.

A consistent estimator is one that becomes more accurate as we increase the sample size. Think of it like getting more guesses in the candy jar game - the more guesses you make, the closer you're likely to get to the real number of candies. In statistics, if we can keep improving our estimate by taking more and more samples, we say that our estimator is consistent.

So, in summary, a consistent estimator is like a guessing game where we keep guessing until we get better and better at it. In statistics, it means that our estimate becomes more accurate as we increase the sample size.