Correlation function (statistical mechanics)

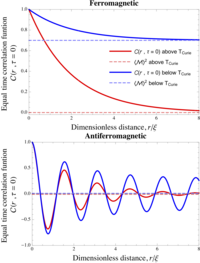
Imagine you have a group of friends who like to play basketball. Sometimes they all play together, but other times they split up into two teams and play against each other. Now, let's suppose you want to know how well your friends play together. You might start by looking at how much each person scores in the games they play.

But what if you want to know how well one player's performance is related to another player's performance? That's where the correlation function comes in. It's like a special formula you can use to see if two things are related to each other.

In our basketball example, you might use the correlation function to see if there's a connection between how many points one person scores and how many points another person scores. If there is a strong relationship between the two, the correlation function will give you a number close to 1. If there is no relationship, the correlation function will give you a number close to 0.

Now, in statistical mechanics, we use the correlation function to study the relationship between the positions and velocities of particles in a system. We want to see if the movements of one particle affect the movements of another particle. If there is a strong correlation, we know that the particles are interacting with each other in some way.

To get more technical, the correlation function is actually a way of measuring the average of the product of two variables at different times or distances. This helps us to see how the variables are changing over time or space, and whether they are related to each other.

So, just like using the correlation function to study basketball games, we can use it in statistical mechanics to study the behavior of particles in a system. It helps us to understand how they move and interact with each other.