Differentiation of trigonometric functions

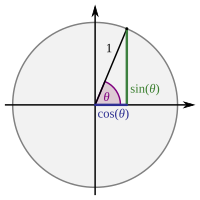
When you walk, you are moving in a specific way that can be described as a set of steps or movements. Similarly, when we talk about trigonometric functions, like sine, cosine, and tangent, we are talking about specific ways of moving or changing in a mathematical sense.

Differentiation is a way to measure how much something changes over time (or in math terms, how much a function changes as you move along its input values). When we differentiate a trigonometric function, we are basically finding out how much it is changing at a specific point (imagine measuring how fast you are walking at a certain point on your walk).

For example, let's say we have a sinusoidal curve (a wave-like shape) that represents a certain phenomenon, such as the way sound waves or light waves move through space. If we want to know how much that wave changes or "slopes" at a certain point, we would use differentiation.

To differentiate a trigonometric function like sine or cosine, we use special rules that help us find the slope at any point along the curve. These rules involve taking the derivative (or the rate of change) of the function using calculus.

Thankfully, we don't need to know all the details of calculus to grasp the basic idea of differentiation. Essentially, we are measuring how much the function is changing, and the math behind it helps us do that quickly and accurately.

So, to recap: trigonometric functions describe specific ways of changing or moving mathematically, and differentiation measures how much they are changing at any given point. By using calculus, we can find the exact slope or rate of change of these functions, which helps us better understand the behavior of waves, oscillations, and other phenomena in the natural world.