Dixon elliptic functions

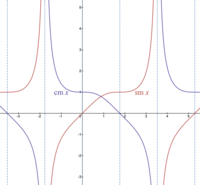
Okay kiddo, let's start with some basic information. Dixon Elliptic Functions are mathematically complex functions that are used to describe certain curves called elliptic curves.

These functions are named after a mathematician named Alfred Cardew Dixon. He studied these functions in the 19th century and found some interesting properties about them.

Imagine you are drawing a circle, but instead of using a compass, you use a ruler to draw straight lines. The shape you get is called an ellipse. Elliptic curves are similar to ellipses, but they have a more complicated structure.

Scientists and mathematicians use Dixon Elliptic Functions to study these elliptic curves. These functions help them understand the behavior of the curves and solve equations related to them.

One interesting thing about Dixon Elliptic Functions is that they are periodic, meaning they repeat over and over again in a predictable way. This makes them useful for modeling things that repeat or have cycles, like the movement of planets or the behavior of waves.

So, to sum it up, Dixon Elliptic Functions are a special kind of math function used to study elliptic curves. They help scientists and mathematicians understand the behavior of these curves and solve equations related to them.