Extended complex plane

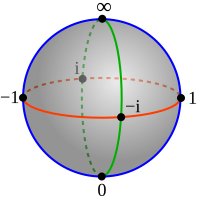
The extended complex plane is like a big piece of paper with lots of numbers on it. Imagine you have a toy airplane that can fly over this big piece of paper, and land on any number it wants.

But some numbers are special, because they are not like the other numbers. For example, imagine you have 3 apples in your basket. That's a normal number, right? But what if I asked you how many apples you have if you don't have any apples at all?

Well, that's a trick question, because you can't have negative apples. It just doesn't make sense.

In the same way, some numbers on this big piece of paper are not like normal numbers because they don't make sense. We call these special numbers "infinity", and they live at the very top and very bottom of the paper.

Now, imagine you are flying your toy airplane over this big piece of paper, and you keep going up and up and up, getting closer and closer to the top. The numbers you land on get bigger and bigger and bigger, until eventually they reach infinity.

This is where the extended complex plane is useful. It helps us understand how numbers behave when they get really, really big or really, really small. And it helps us understand that some numbers just don't make sense in the same way that negative apples don't make sense.