Inverse hyperbolic function
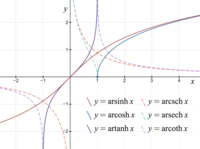
Okay kiddo, let's talk about inverse hyperbolic functions. Remember how we talked about the hyperbolic functions before? These are functions like sinh, cosh, and tanh that work a bit differently than regular trigonometric functions. Well, the inverse hyperbolic function is kind of like the opposite of those!
The inverse hyperbolic function, also known as an arc-hyperbolic function or arc-hyperbolic cosine, is a function that helps you find the angle that corresponds to a certain value of a hyperbolic function. So, let's say you know the value of cosh(x) and you want to find out what x is. You can use the inverse hyperbolic cosine function (cosh^-1), also written as arccosh, to help you figure it out!
It might sound a bit confusing, but think of it like this: if you know that cosh(x) is equal to some number y, then arccosh(y) will give you the value of x. It's like you're undoing the cosh function to get back the original value of x.
The same goes for other hyperbolic functions too. If you know the value of sinh(x) or tanh(x), you can use the inverse hyperbolic sine function (sinh^-1), also written as arcsinh, or the inverse hyperbolic tangent function (tanh^-1), also written as arctanh, to find the corresponding value of x.
So, to sum it up, inverse hyperbolic functions are like a special tool you can use to find an angle (or value of x) that corresponds to a specific value of a hyperbolic function. It's like a secret code that helps you undo the hyperbolic function and solve equations in a different way!
The inverse hyperbolic function, also known as an arc-hyperbolic function or arc-hyperbolic cosine, is a function that helps you find the angle that corresponds to a certain value of a hyperbolic function. So, let's say you know the value of cosh(x) and you want to find out what x is. You can use the inverse hyperbolic cosine function (cosh^-1), also written as arccosh, to help you figure it out!
It might sound a bit confusing, but think of it like this: if you know that cosh(x) is equal to some number y, then arccosh(y) will give you the value of x. It's like you're undoing the cosh function to get back the original value of x.
The same goes for other hyperbolic functions too. If you know the value of sinh(x) or tanh(x), you can use the inverse hyperbolic sine function (sinh^-1), also written as arcsinh, or the inverse hyperbolic tangent function (tanh^-1), also written as arctanh, to find the corresponding value of x.
So, to sum it up, inverse hyperbolic functions are like a special tool you can use to find an angle (or value of x) that corresponds to a specific value of a hyperbolic function. It's like a secret code that helps you undo the hyperbolic function and solve equations in a different way!
Related topics others have asked about:
