Japanese theorem for concyclic quadrilaterals

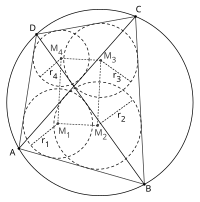
Okay, so imagine there’s a playground with four points on the edges. If we “connect the dots” with lines, we’ll have four sides making a shape like a square or rectangle. This shape is called a quadrilateral.

Now, let’s say that we drew a circle around the playground. If all four corners of the quadrilateral touch the circle, that means it’s a concyclic quadrilateral. That’s a fancy way of saying that all the points that make up the shape fit neatly on the circle - like a puzzle piece fitting perfectly in its spot.

The Japanese Theorem for concyclic quadrilaterals basically says that if we draw certain lines inside the concyclic quadrilateral, the points where those lines cross will form a new quadrilateral - and this new quadrilateral will also be concyclic!

The lines we draw are called diagonals, and they go from one corner of the quadrilateral to the opposite corner. So if we connect the top left corner to the bottom right corner, and the top right corner to the bottom left corner, we’ve drawn the diagonals.

Now, the Japanese Theorem tells us that the point where the lines cross will be a new corner of another quadrilateral that’s also on the circle. This new quadrilateral won’t always look exactly like the original one - it might be stretched out in a different direction or have different angles. But it will always be concyclic too, meaning all four corners touch the circle.

This theorem can be used to solve all sorts of geometry problems involving concyclic quadrilaterals. Pretty cool, huh?