Legendre polynomials
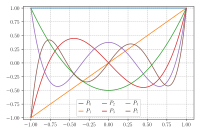
Legendre polynomials are special kinds of math equations that can be used to solve problems involving waves, heat, and other things in science and engineering. They were named after a French mathematician named Adrien-Marie Legendre who first came up with them back in the 18th century.
Now, imagine you are riding on a big wave in the ocean. The wave can go up and down, and it has a certain shape that repeats itself over and over. This shape is called a "waveform." Legendre polynomials can be used to describe these waveforms mathematically, so that scientists and engineers can study them and understand how they behave.
Legendre polynomials are made up of a series of terms, each of which has a different "degree." The degree of a term tells you how many times a certain variable (usually x) is multiplied by itself in that term. For example, the term x^2 has a degree of 2, because x is multiplied by itself twice.
The first few Legendre polynomials have special names and formulas. The first one, P_0(x) (pronounced "P-sub-zero of x"), is just equal to 1. The second one, P_1(x), is equal to x. The third one, P_2(x), is a little more complicated, but it looks like this:
P_2(x) = (3x^2 - 1)/2.
As you can see, each Legendre polynomial gets more and more complicated as the degree of its terms increases. But no matter how high the degree is, Legendre polynomials always have some important properties that make them useful for scientists and engineers. For example, they are "orthogonal," which means that when you multiply two different Legendre polynomials together and integrate them over a certain range, you get zero. This property makes it easier to solve certain kinds of equations that involve Legendre polynomials.
In summary, Legendre polynomials are special kinds of math equations that are used to describe waveforms and other phenomena in science and engineering. They are made up of a series of terms with different degrees, and they have important properties that make them useful for solving equations.
Now, imagine you are riding on a big wave in the ocean. The wave can go up and down, and it has a certain shape that repeats itself over and over. This shape is called a "waveform." Legendre polynomials can be used to describe these waveforms mathematically, so that scientists and engineers can study them and understand how they behave.
Legendre polynomials are made up of a series of terms, each of which has a different "degree." The degree of a term tells you how many times a certain variable (usually x) is multiplied by itself in that term. For example, the term x^2 has a degree of 2, because x is multiplied by itself twice.
The first few Legendre polynomials have special names and formulas. The first one, P_0(x) (pronounced "P-sub-zero of x"), is just equal to 1. The second one, P_1(x), is equal to x. The third one, P_2(x), is a little more complicated, but it looks like this:
P_2(x) = (3x^2 - 1)/2.
As you can see, each Legendre polynomial gets more and more complicated as the degree of its terms increases. But no matter how high the degree is, Legendre polynomials always have some important properties that make them useful for scientists and engineers. For example, they are "orthogonal," which means that when you multiply two different Legendre polynomials together and integrate them over a certain range, you get zero. This property makes it easier to solve certain kinds of equations that involve Legendre polynomials.
In summary, Legendre polynomials are special kinds of math equations that are used to describe waveforms and other phenomena in science and engineering. They are made up of a series of terms with different degrees, and they have important properties that make them useful for solving equations.
Related topics others have asked about:
