Line segment intersection
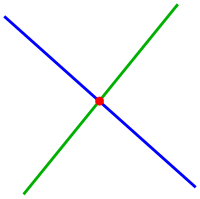
Imagine you have two straight lines drawn on a piece of paper. Let's call them Line A and Line B. Line A has two points on it, let's say Point X and Point Y. Line B also has two points, Point Z and Point W.
If we draw these lines and points on the same piece of paper, we can see that they might cross each other at some point. When two lines cross, they create an intersection point.
However, not all lines cross each other. Sometimes they are parallel, meaning they run next to each other in the same direction and will never cross.
When we talk about line segment intersection, we are interested in finding out whether the two lines actually cross each other and where they intersect.
To figure this out, we use something called coordinate geometry. We can assign a set of x and y coordinates to each of the four points on the two lines.
For example, Point X might be at (2,5), meaning it is 2 units to the right and 5 units up from the origin (which is usually the bottom left corner of the paper). Point Z might be at (-1,2) which is 1 unit to the left and 2 units up from the origin.
Once we have these coordinates, we can use mathematical equations to figure out whether the lines cross and where the intersection point is.
This involves some algebra and solving equations, but essentially we are looking for a point where the x and y coordinates of both lines are equal.
If we find this point, we know that the lines intersect at that point. If we can't find such a point, we know that the lines are either parallel or don't cross each other.
Overall, line segment intersection is a way to figure out whether two lines on a piece of paper cross each other and where they meet. We use math and coordinates to do this.
If we draw these lines and points on the same piece of paper, we can see that they might cross each other at some point. When two lines cross, they create an intersection point.
However, not all lines cross each other. Sometimes they are parallel, meaning they run next to each other in the same direction and will never cross.
When we talk about line segment intersection, we are interested in finding out whether the two lines actually cross each other and where they intersect.
To figure this out, we use something called coordinate geometry. We can assign a set of x and y coordinates to each of the four points on the two lines.
For example, Point X might be at (2,5), meaning it is 2 units to the right and 5 units up from the origin (which is usually the bottom left corner of the paper). Point Z might be at (-1,2) which is 1 unit to the left and 2 units up from the origin.
Once we have these coordinates, we can use mathematical equations to figure out whether the lines cross and where the intersection point is.
This involves some algebra and solving equations, but essentially we are looking for a point where the x and y coordinates of both lines are equal.
If we find this point, we know that the lines intersect at that point. If we can't find such a point, we know that the lines are either parallel or don't cross each other.
Overall, line segment intersection is a way to figure out whether two lines on a piece of paper cross each other and where they meet. We use math and coordinates to do this.
Related topics others have asked about:
