Linear independence

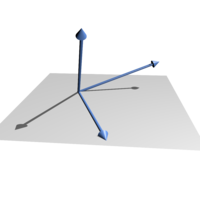
Okay kiddo, imagine you have a bunch of different toys. Let's say you have a teddy bear, a ball, and a toy car.

Now imagine you have to decide if these toys are "linearly independent." That means, if you can make one toy by stretching, squishing, or mixing the other toys together.

If you can't make any of the toys from the others, then they are "linearly independent."

So in this case, the teddy bear, the ball, and the toy car are all different and can't be made from stretching or mixing the others. So they are linearly independent!

Just like with toys, in math we use linear independence to see if a group of numbers, called vectors, are all different or if some of them can be made from stretching or mixing the others.

It's kind of like having a bunch of different building blocks. If each block is unique and can't be made from a combination of other blocks, then they are linearly independent.

And just like with toys and building blocks, being linearly independent is a good thing in math because it means we have a strong foundation to build upon.