Maximum spacing estimation
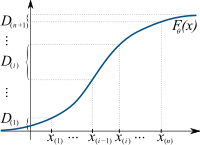
Okay, imagine you have a lot of toys, like cars, dolls, and blocks. You want to put all of them in a box, but you don't want the box to be too full or too empty. You want the box to be just right with enough space for all your toys to fit comfortably.
The maximum spacing estimation is kind of like that. Instead of toys, we have numbers, and we want to put them in a line or a sequence. We want to know the right amount of space or distance to leave between each number so that they're not too close together and not too far apart.
This is important for many things, like programming, statistics, and data analysis. It helps us make sure that our numbers are organized and easy to read, which is really helpful when we need to use them for something important.
To find the maximum spacing estimation, we use a special formula or equation. We look at the numbers we have and figure out what the biggest difference is between them. Then we divide that difference by the number of spaces between the numbers (minus one).
Let's say we have the numbers 1, 4, 7, and 10. The biggest difference between these numbers is 9 (10 minus 1). We have 3 spaces between the numbers, so we subtract 1 from 3 to get 2. Then we divide 9 by 2 to get 4.5.
That means we should leave 4.5 units of space between each number to make sure they're evenly spaced and easy to read. If we put them too close together, they might be hard to tell apart. If we put them too far apart, they might look like they're not related to each other.
So, that's the maximum spacing estimation. It's like finding the right amount of space between your toys in a toy box, except with numbers in a line. It helps us keep things organized and easy to read.
The maximum spacing estimation is kind of like that. Instead of toys, we have numbers, and we want to put them in a line or a sequence. We want to know the right amount of space or distance to leave between each number so that they're not too close together and not too far apart.
This is important for many things, like programming, statistics, and data analysis. It helps us make sure that our numbers are organized and easy to read, which is really helpful when we need to use them for something important.
To find the maximum spacing estimation, we use a special formula or equation. We look at the numbers we have and figure out what the biggest difference is between them. Then we divide that difference by the number of spaces between the numbers (minus one).
Let's say we have the numbers 1, 4, 7, and 10. The biggest difference between these numbers is 9 (10 minus 1). We have 3 spaces between the numbers, so we subtract 1 from 3 to get 2. Then we divide 9 by 2 to get 4.5.
That means we should leave 4.5 units of space between each number to make sure they're evenly spaced and easy to read. If we put them too close together, they might be hard to tell apart. If we put them too far apart, they might look like they're not related to each other.
So, that's the maximum spacing estimation. It's like finding the right amount of space between your toys in a toy box, except with numbers in a line. It helps us keep things organized and easy to read.
Related topics others have asked about:
