Microstate (statistical mechanics)

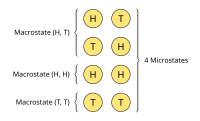
A microstate in statistical mechanics is like a game of Legos. Imagine you have lots of tiny Legos and you want to build something cool. You start putting the Legos together in different ways until you have lots of different structures. Each of these structures is a "microstate."

Now imagine you don't have just a few Legos, but MILLIONS of them. There are so many different ways you can put them together to make all sorts of cool things. In the same way, when you have lots of tiny particles - like atoms or molecules - you can put them together in many different ways to make different microstates.

For example, imagine you have a bunch of ping pong balls bouncing around in a box. Each ping pong ball is a particle, and the way they bounce around in the box is a microstate. Some microstates might have all the ping pong balls clustered together, while others might have them bouncing all over the place.

The cool thing about microstates is that they follow certain rules. These rules are called the laws of thermodynamics, and they help us understand how the microstates behave. For example, one of the laws says that the total energy of the microstate always stays the same. Another law says that the entropy of the microstate (which is a way of measuring how "disordered" or "random" it is) tends to increase over time.

So, in summary, a microstate in statistical mechanics is like a Lego creation or a bouncing ping pong ball system. It's one possible arrangement of tiny particles (like atoms or molecules) that follow certain rules, and we use the laws of thermodynamics to understand how they behave.