Osculating circle

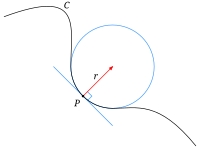
An osculating circle is like the best-fitting circle you can draw on a curve. You know how if you draw a curve with a pencil, it might be a little wiggly and not perfectly smooth? Well, the osculating circle helps us to understand how the curve is changing at each point, and gives us a way to measure things like the curve's slope and curvature.

Here's an example: imagine you're riding a bicycle along a windy road that curves and twists a lot. As you ride, you might feel like you're leaning to the left or right depending on the shape of the road. The curve of the road is what we're talking about when we say "osculation."

To find the osculating circle for a given point on a curve, we start by drawing a tangent line (remember, that's a line that just touches the curve at one point). Then we draw a line perpendicular to the tangent line, which will be our radius. Now we can draw a circle with that radius, and voila! That's our osculating circle.

The shape of the osculating circle will change depending on where we draw it on the curve. If the curve is really curvy, the osculating circle might be small and tight. But if the curve is flatter, the osculating circle might be bigger and more spread out.

So why do mathematicians care about osculating circles? Well, they can help us to understand lots of things, like the behavior of planets and satellites as they move through space, or the way that rivers shape the landscape over time. By studying the osculating circles of curves, we can learn more about the world around us and the patterns that shape it.