Tubular neighborhood
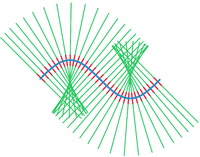
Imagine you are holding a bunch of straws in your hand. Now, imagine you can pick any one of these straws and draw a big circle around it on a paper. This circle will form what is called a "tubular neighborhood" of the straw.
Similarly, in math, a tubular neighborhood is formed around a one-dimensional shape (like a curve or a line) in a higher-dimensional space (like a 2D or 3D space). This shape is formed by drawing a big "tube" around the original, one-dimensional shape, so that it becomes a bigger, higher-dimensional shape.
For example, if you imagine a squiggly 1D shape on a flat surface and draw a tube around it that extends equally in all directions, it will form a shape that looks like a straw, similar to the one you imagined earlier. This tube is called the "tubular neighborhood" of the original curve.
In essence, a tubular neighborhood is a way to describe the space around a one-dimensional object in a higher-dimensional space, and it is useful in the study of geometry, topology, and other areas of mathematics.
Similarly, in math, a tubular neighborhood is formed around a one-dimensional shape (like a curve or a line) in a higher-dimensional space (like a 2D or 3D space). This shape is formed by drawing a big "tube" around the original, one-dimensional shape, so that it becomes a bigger, higher-dimensional shape.
For example, if you imagine a squiggly 1D shape on a flat surface and draw a tube around it that extends equally in all directions, it will form a shape that looks like a straw, similar to the one you imagined earlier. This tube is called the "tubular neighborhood" of the original curve.
In essence, a tubular neighborhood is a way to describe the space around a one-dimensional object in a higher-dimensional space, and it is useful in the study of geometry, topology, and other areas of mathematics.
Related topics others have asked about:
