Vector fields in cylindrical and spherical coordinates
Imagine you are at a park and there are lots of kids everywhere. Now, imagine you want to keep track of where all the kids are going. You can draw arrows on the ground that show which direction each kid is going. These arrows can start at the point where the kid is standing and go in the direction that they are moving.
Now, let's imagine that instead of kids in a park, we are looking at something called a "vector field." This is a bunch of arrows that show the direction and strength of some physical quantity, like wind or water flow, at each point in space.
To understand vector fields in cylindrical and spherical coordinates, we need to know a little bit about how we describe points in space.
In cylindrical coordinates, instead of using x, y, and z coordinates, we use something called "r," which is the distance from the origin (like the center of a circle), and "theta," which is the angle that you need to turn from the x-axis to get to the point.
Now, let's imagine we are looking at a vector field that represents the wind speed at each point in space. We can draw arrows at each point that show the direction and magnitude of the wind speed. In cylindrical coordinates, each arrow has two components: a magnitude (how fast the wind is blowing), and an angle (which direction the wind is blowing in). We can write this as (magnitude, angle).
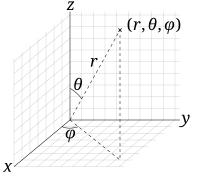
In spherical coordinates, we again use "r," but we also use two angles: "theta," which is the angle you turn from the positive x-axis to get to the point, and "phi," which is the angle from the positive z-axis to the point.
For a vector field in spherical coordinates, each arrow again has two components: magnitude and direction. But now, instead of just a single angle, we have two angles that determine the direction of the arrow. We can write this as (magnitude, theta, phi).
So, to summarize: vector fields are a bunch of arrows that show the direction and magnitude of some physical quantity at each point in space. In cylindrical coordinates, we use distance and angle to describe points, and each arrow has two components: magnitude and angle. In spherical coordinates, we use distance and two angles to describe points, and each arrow has three components: magnitude, theta, and phi.
Now, let's imagine that instead of kids in a park, we are looking at something called a "vector field." This is a bunch of arrows that show the direction and strength of some physical quantity, like wind or water flow, at each point in space.
To understand vector fields in cylindrical and spherical coordinates, we need to know a little bit about how we describe points in space.
In cylindrical coordinates, instead of using x, y, and z coordinates, we use something called "r," which is the distance from the origin (like the center of a circle), and "theta," which is the angle that you need to turn from the x-axis to get to the point.
Now, let's imagine we are looking at a vector field that represents the wind speed at each point in space. We can draw arrows at each point that show the direction and magnitude of the wind speed. In cylindrical coordinates, each arrow has two components: a magnitude (how fast the wind is blowing), and an angle (which direction the wind is blowing in). We can write this as (magnitude, angle).
In spherical coordinates, we again use "r," but we also use two angles: "theta," which is the angle you turn from the positive x-axis to get to the point, and "phi," which is the angle from the positive z-axis to the point.
For a vector field in spherical coordinates, each arrow again has two components: magnitude and direction. But now, instead of just a single angle, we have two angles that determine the direction of the arrow. We can write this as (magnitude, theta, phi).
So, to summarize: vector fields are a bunch of arrows that show the direction and magnitude of some physical quantity at each point in space. In cylindrical coordinates, we use distance and angle to describe points, and each arrow has two components: magnitude and angle. In spherical coordinates, we use distance and two angles to describe points, and each arrow has three components: magnitude, theta, and phi.
Related topics others have asked about:
