multiple integral

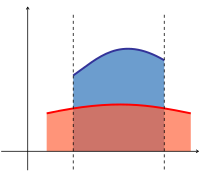
Imagine you have a big pizza, divided into many slices. Each slice has a different flavor, and each flavor corresponds to a number that tells you how much that slice is worth.

Now, imagine you want to know how much the whole pizza is worth. You could add up all the numbers for each slice, but that would take a long time, especially if you have a lot of slices.

Instead, you can use something called a multiple integral. This is like a special tool that helps you add up all the numbers for each slice, without having to do it one slice at a time.

To use the multiple integral, you start at the bottom of the pizza and work your way up, adding up the numbers for each slice as you go. But instead of adding up in a straight line, you move in two directions at once.

First, you move in the direction of the slices (horizontally), and then you move in the direction of the crust (vertically). Each time you move a little bit in each direction, you add up the number for the slice you're on.

If you keep doing this, moving a little bit in each direction and adding up the numbers as you go, you will eventually cover the entire pizza and end up with the total value of the pizza.

This might sound complicated, but it's actually a very useful tool for solving all kinds of problems in math and science. And if you ever get confused, just remember: it's like adding up the numbers on a pizza, one slice at a time, but with a special tool that helps you do it faster!