Complex analysis
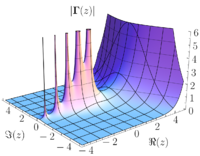
Complex analysis is a branch of mathematics that deals with numbers that are made up of a combination of two parts: real numbers and imaginary numbers. These numbers are also called complex numbers.
Real numbers are the numbers that we usually use in everyday life, like 0, -3, 0.5, or √2. They are called "real" because they can be represented on a straight line, called the number line.
Imaginary numbers, on the other hand, are numbers that we can't represent on the number line. They are numbers that are a multiple of the square root of -1 (represented by the letter "i"). For example, 2i, -3i, or √(-1) are all imaginary numbers.
Complex numbers are a combination of real and imaginary numbers. They can be written in the form a + bi, where "a" and "b" are real numbers.
What makes complex analysis interesting is that it allows us to study functions that involve complex numbers. A function is a mathematical rule that takes an input and produces an output.
For example, a simple function could be f(x) = x^2. If we plug in x = 3, we get f(3) = 9 as an output. Complex analysis deals with functions that take complex numbers as inputs and produce complex numbers as outputs.
One of the most famous functions in complex analysis is called the complex exponential function. It is a function that takes a complex number z as an input and produces a new complex number ez as an output. The complex exponential function has many interesting properties and is used in many areas of mathematics and science.
Another important concept in complex analysis is the idea of a complex plane. A complex plane is a two-dimensional plane where each point represents a complex number. We can plot complex numbers on this plane just as we plot points on a regular graph.
In complex analysis, we study how functions behave when we plot them on the complex plane. For example, some functions may create patterns that repeat themselves in a regular way, while others may create chaotic patterns that are impossible to predict in advance.
Overall, complex analysis is a fascinating and powerful tool that allows us to understand functions that involve complex numbers. It has many applications in fields like physics, engineering, and computer science.
Real numbers are the numbers that we usually use in everyday life, like 0, -3, 0.5, or √2. They are called "real" because they can be represented on a straight line, called the number line.
Imaginary numbers, on the other hand, are numbers that we can't represent on the number line. They are numbers that are a multiple of the square root of -1 (represented by the letter "i"). For example, 2i, -3i, or √(-1) are all imaginary numbers.
Complex numbers are a combination of real and imaginary numbers. They can be written in the form a + bi, where "a" and "b" are real numbers.
What makes complex analysis interesting is that it allows us to study functions that involve complex numbers. A function is a mathematical rule that takes an input and produces an output.
For example, a simple function could be f(x) = x^2. If we plug in x = 3, we get f(3) = 9 as an output. Complex analysis deals with functions that take complex numbers as inputs and produce complex numbers as outputs.
One of the most famous functions in complex analysis is called the complex exponential function. It is a function that takes a complex number z as an input and produces a new complex number ez as an output. The complex exponential function has many interesting properties and is used in many areas of mathematics and science.
Another important concept in complex analysis is the idea of a complex plane. A complex plane is a two-dimensional plane where each point represents a complex number. We can plot complex numbers on this plane just as we plot points on a regular graph.
In complex analysis, we study how functions behave when we plot them on the complex plane. For example, some functions may create patterns that repeat themselves in a regular way, while others may create chaotic patterns that are impossible to predict in advance.
Overall, complex analysis is a fascinating and powerful tool that allows us to understand functions that involve complex numbers. It has many applications in fields like physics, engineering, and computer science.
Related topics others have asked about:
