Diophantine approximation

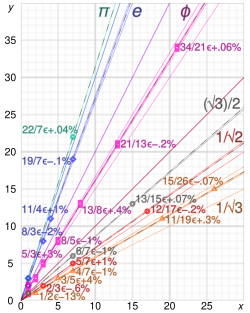
Diophantine approximation is a process of finding fractions (numbers like 1/2 or 7/3) that are very close to each other. For example, 3/5 and 4/6 are Diophantine approximations because they are very close together. To find Diophantine approximations, we use something called the Euclidean algorithm, which is a fancy way of doing calculations. We start by picking two numbers that we want to approximate, for example 5 and 7. Then, we divide 5 by 7 to get 0.714. We then subtract that number from 5 to get 4.7. We then divide 4.7 by 7 to get 0.678. We then subtract that from 5 to get 4.3 and so on. When we find a number in the sequence that looks like a fraction such as 4/7, then 4/7 is our Diophantine approximation for 5/7.