Dirac delta function

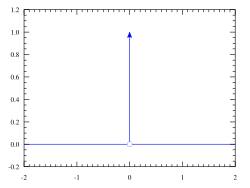
The Dirac delta function is a special function that is often used in math and physics. It is imaginary (like a pretend friend), but it helps us solve problems that deal with extremely concentrated forces or impulses, such as when a hammer strikes a nail.

Imagine you have a tiny toy hammer that you use to hit a tiny nail. The force from the hammer is very strong but only affects a tiny spot. Now imagine that toy hammer getting smaller and smaller, until it's so small that it's almost like a point. When you hit the nail with that point, the force becomes super concentrated at that exact point. This is similar to what the Dirac delta function does - it represents an infinitely strong and short force (or impulse) at a single point.

But a problem with this toy hammer example is that we can only measure forces over distances, not at a single point. So, the Dirac delta function is used to represent this concentrated force as a limit of a sequence of functions that approach zero everywhere except for an area around that point. This is like pretending that the force is very strong but very short lived.

So, the Dirac delta function is a very special function that is like a pretend friend we use to solve problems that involve very strong and short forces. It's not real, but it helps us understand the world around us a little better.