Donsker's theorem

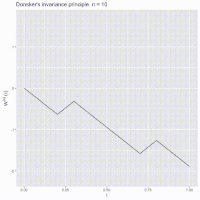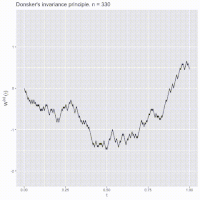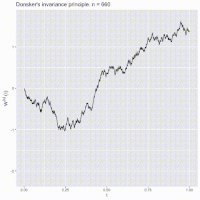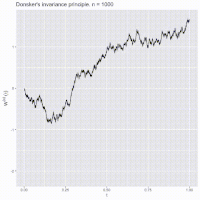
Okay kiddo, so here's a fun story about something called Donsker's Theorem.

Imagine you're going for a walk around your neighborhood, and you see a group of ants walking in a line. They all look kind of random and chaotic, walking in different directions and bumping into each other. But if you zoom out and watch them for a while, you might notice that over time they start to look like they're all moving in the same direction, almost like they're a big ant "wave" moving across the ground.

Well, mathematicians like to study patterns like this, and one guy named Michael Donsker came up with a special rule that helps us describe how random-looking things can start to look more and more predictable over time.

Basically, if you take a bunch of random numbers (or "walks") and keep adding them up as you go along, you end up with a big ol' line that looks really chaotic and zig-zaggy at first. But if you KEEP adding up more and more numbers (like watching those ants for a long time), eventually that line starts to smooth out and look more like a straight line.

And Donsker's Theorem says that this pattern happens a LOT, not just with ants or random walks, but with all kinds of things in math and science. So even if it seems like you can't predict what'll happen next, if you look at enough data over a long enough time, you may be able to see a pattern emerge. Cool, right?