Finite difference time domain

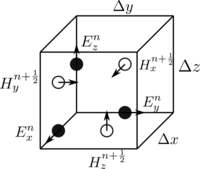
Imagine you have a toy car on a track and you want to figure out how it moves over time. This is kind of what people use finite difference time domain (FDTD) for but instead of a toy car, they use electric and magnetic fields on a grid.

The grid is like a map or a graph with a lot of little squares, kind of like a checkerboard. Each of these squares is called a cell and it has an electric and magnetic field inside of it. These fields are what we use to figure out how everything moves over time.

To figure out what happens in each cell over time, we need to break time up into small chunks. Think of it like a movie where we see one frame at a time. We take one little step forward in time and see how the electric and magnetic fields change in each cell. Then we take another step forward in time and see how things have changed again.

But how do we know how things change from one step to the next? We use something called finite difference equations. These are like rules or instructions that tell us how to update the electric and magnetic fields in each cell based on what they were before and what's happening around them.

To make sure our calculations are right, we also need to make sure the rules we use are accurate enough. This means checking they give us answers that are similar to what we would expect in real life. We might do this by running experiments with toy cars or by comparing our results to other methods.

Using FDTD can help us figure out all sorts of things like how light moves through different materials, how microwaves travel through space, or even how to design better antennas. It's like having a really powerful microscope for electricity and magnetism.