Independence (probability theory)

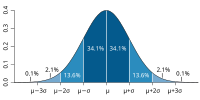
Alright kiddo, we are going to talk about independence in probability theory.

Let's imagine you have a bag full of colored balls - red, blue, and green. Now, let's say you pick a ball out of the bag, and you put it aside.

If you reach into the bag again, the probability (chance) of picking out a red ball is different now. Why? Because you already took one out of the bag!

But let's say you put the first ball back into the bag before picking again. If you do this, then the probability of picking out a red ball the second time is exactly the same as the first time.

This is what we call independence in probability. If the outcome of one event doesn't affect the outcome of another event, then we say they are independent. If the first event does affect the second event, then we say they are dependent.

So in our example, the second event (picking again) is independent from the first event (picking and putting aside the first ball) if we put the first ball back into the bag.

Does that make sense, kiddo?