Inner product
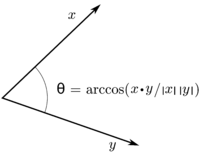
An inner product is like a secret handshake between two numbers that lets them say how much they like each other. It's a special kind of multiplication that takes two numbers, let's call them A and B, and gives us a new number that tells us how much they have in common.
Imagine we have two numbers, like 3 and 5. We can multiply them together and get 15. But if we use an inner product, we get a different answer. We can write it like this: <3, 5>. That little symbol in the middle is called an inner product symbol.
Now, let's say A is a bunch of numbers: <2, 3, 1>. And B is another bunch of numbers: <1, 2, 3>. We can use the inner product to find out how much they have in common. We multiply the first numbers (2 and 1) and add them to the product of the second numbers (3 and 2), and add that to the product of the third numbers (1 and 3). It looks like this:
<2, 3, 1> · <1, 2, 3> = (2 * 1) + (3 * 2) + (1 * 3) = 2 + 6 + 3 = 11
So the inner product of A and B is 11. This tells us that they have some things in common, but not everything. It's like two friends who enjoy the same TV shows, but not all of them.
Inner products are really useful in math because they can help us measure how similar or dissimilar two things are. If we have a bunch of data points, we can use an inner product to see which ones are more similar to each other. It's kind of like a secret code that lets numbers talk to each other.
Imagine we have two numbers, like 3 and 5. We can multiply them together and get 15. But if we use an inner product, we get a different answer. We can write it like this: <3, 5>. That little symbol in the middle is called an inner product symbol.
Now, let's say A is a bunch of numbers: <2, 3, 1>. And B is another bunch of numbers: <1, 2, 3>. We can use the inner product to find out how much they have in common. We multiply the first numbers (2 and 1) and add them to the product of the second numbers (3 and 2), and add that to the product of the third numbers (1 and 3). It looks like this:
<2, 3, 1> · <1, 2, 3> = (2 * 1) + (3 * 2) + (1 * 3) = 2 + 6 + 3 = 11
So the inner product of A and B is 11. This tells us that they have some things in common, but not everything. It's like two friends who enjoy the same TV shows, but not all of them.
Inner products are really useful in math because they can help us measure how similar or dissimilar two things are. If we have a bunch of data points, we can use an inner product to see which ones are more similar to each other. It's kind of like a secret code that lets numbers talk to each other.
Related topics others have asked about:
