Lagrangian and Eulerian coordinates

Imagine you are playing with a toy boat in a bathtub full of water. When you move the boat around with your hand, you can describe its movement in two different ways.

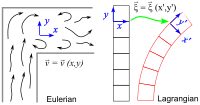
The first way is called Lagrangian coordinates. Imagine you have a friend standing next to the bathtub, watching the boat move. Your friend can keep track of where the boat is at any given moment and how fast it is going. Your friend can describe the boat's movement entirely based on the boat's position and velocity. This is like playing with the boat using your hand to move it directly.

The second way is called Eulerian coordinates. Imagine you have a camera on the ceiling above the bathtub, recording the water's movement. When you play back the video, you can see how the water is moving, and you can see the boat moving in relation to the water. You can describe the boat's movement based on the water's movement around it. This is like watching the boat move while the water moves around it.

In short, Lagrangian coordinates follow the movement of an object as it moves around while Eulerian coordinates describe the movement of an object relative to the fixed coordinates of the frame of reference.