Parallel postulate

Imagine you have a piece of paper and a ruler. If you draw a straight line on the paper, you know that line will go on forever in both directions. This is called a "straight line" and it's really important in math.

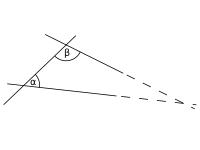
Now, let's say you have two more lines. These lines are also straight, but they're not on the same line as the first one. If you extend these lines, you might notice something really interesting. These lines will either:

1. never ever meet
2. meet once
3. or meet many times

But what if there was a chance that these lines would meet at some point without ever crossing each other? That's what the parallel postulate is all about.

The parallel postulate says that if you have a line and a point, you can draw exactly one line that is parallel to the first one and goes through that point. This means that two parallel lines will never ever meet, no matter how far they go.

This might seem simple but it's actually a really big deal. Mathematicians spent a long time trying to prove this postulate, or find a way to make it true without it being taken for granted. It was finally proven by Euclid, an Ancient Greek mathematician, in his book "Elements."

So the parallel postulate is a rule that says straight lines will either never meet, meet once, or meet many times, but will never cross over each other.