Partition function (number theory)
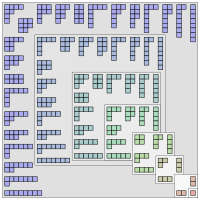
The partition function in number theory is like a cooking recipe. Imagine you have a lot of apples and you want to divide them up into groups of different sizes. The partition function tells you how many different ways you can divide up the apples into groups of different sizes.
Let's say you have 4 apples. You could divide them up into:
- 1 group of 4 apples
- 2 groups of 2 apples each
- 1 group of 3 apples and 1 group of 1 apple
- 1 group of 1 apple and 1 group of 3 apples
- 1 group of 2 apples and 2 groups of 1 apple each
- 2 groups of 1 apple each and 1 group of 2 apples
That's a total of 6 different ways to divide up the apples into groups of different sizes. The partition function for 4, denoted as p(4), is equal to 6.
You can do the same thing with larger numbers. Let's say you have 5 apples. You could divide them up into:
- 1 group of 5 apples
- 2 groups of 2 apples each and 1 group of 1 apple
- 1 group of 2 apples and 1 group of 3 apples
- 1 group of 3 apples and 1 group of 2 apples
- 1 group of 1 apple and 1 group of 4 apples
- 1 group of 4 apples and 1 group of 1 apple
- 3 groups of 1 apple each and 1 group of 2 apples
- 2 groups of 1 apple each and 1 group of 3 apples
- 1 group of 1 apple and 1 group of 2 apples and 1 group of 2 apples
- 1 group of 1 apple and 2 groups of 2 apples each
- 2 groups of 1 apple each and 1 group of 1 apple and 1 group of 2 apples
- 2 groups of 1 apple each and 1 group of 1 apple and 1 group of 3 apples
- 4 groups of 1 apple each and 1 group of 1 apple
That's a total of 12 different ways to divide up the apples into groups of different sizes. The partition function for 5, denoted as p(5), is equal to 12.
The partition function is important in number theory because it helps us understand the properties of numbers and their relationships to other numbers. We can use the partition function to see patterns and make predictions about the behavior of numbers. It's like a super useful tool for solving number problems!
Let's say you have 4 apples. You could divide them up into:
- 1 group of 4 apples
- 2 groups of 2 apples each
- 1 group of 3 apples and 1 group of 1 apple
- 1 group of 1 apple and 1 group of 3 apples
- 1 group of 2 apples and 2 groups of 1 apple each
- 2 groups of 1 apple each and 1 group of 2 apples
That's a total of 6 different ways to divide up the apples into groups of different sizes. The partition function for 4, denoted as p(4), is equal to 6.
You can do the same thing with larger numbers. Let's say you have 5 apples. You could divide them up into:
- 1 group of 5 apples
- 2 groups of 2 apples each and 1 group of 1 apple
- 1 group of 2 apples and 1 group of 3 apples
- 1 group of 3 apples and 1 group of 2 apples
- 1 group of 1 apple and 1 group of 4 apples
- 1 group of 4 apples and 1 group of 1 apple
- 3 groups of 1 apple each and 1 group of 2 apples
- 2 groups of 1 apple each and 1 group of 3 apples
- 1 group of 1 apple and 1 group of 2 apples and 1 group of 2 apples
- 1 group of 1 apple and 2 groups of 2 apples each
- 2 groups of 1 apple each and 1 group of 1 apple and 1 group of 2 apples
- 2 groups of 1 apple each and 1 group of 1 apple and 1 group of 3 apples
- 4 groups of 1 apple each and 1 group of 1 apple
That's a total of 12 different ways to divide up the apples into groups of different sizes. The partition function for 5, denoted as p(5), is equal to 12.
The partition function is important in number theory because it helps us understand the properties of numbers and their relationships to other numbers. We can use the partition function to see patterns and make predictions about the behavior of numbers. It's like a super useful tool for solving number problems!
