Runge's phenomenon

Okay kiddo, have you ever played with building blocks like Legos or Magna-Tiles? Say you're building a tower and you're using bigger and bigger blocks as you go up. But suddenly, as you add more blocks, your tower looks wobbly and unstable - even though each block is solid on its own. This is similar to what happens with Runge's phenomenon.

You may have heard of something called polynomial interpolation, which is a way to find a curve that fits a set of data points perfectly. Imagine you have a bunch of dots on a graph, and you want to draw a smooth line that passes through all of them. A polynomial is a type of equation that can do just that.

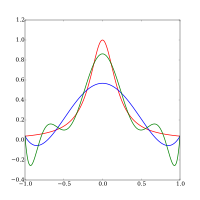
But the problem with polynomial interpolation is that sometimes, when we add more and more data points, the polynomial curve becomes really "wiggly" and starts to look nothing like the original data. It's like trying to build a tower using bigger and bigger blocks, but the tower starts bending and twisting in weird ways because the blocks are too big. This is called Runge's phenomenon.

Why does this happen? Well, imagine you're trying to fit a curve to a set of points where the data is mostly on the edges of the graph. The polynomial tries its best to pass through all of the points, but as it gets closer to the middle, the curve begins to oscillate wildly. This is because higher-degree polynomials have more "wiggle room" to fit the data, but at a cost of becoming more erratic.

So is polynomial interpolation bad? No, it's still a very useful tool in many areas of math and science. But we do have to be careful and make sure we're not using too high-degree polynomials, especially if our data is evenly spaced or clustered around the center of the graph. And that, sweetie, is Runge's phenomenon in a nutshell!